LostintheWoods
Member
The answer is, indeed, "Ol' Jed's a millionaire." "Well, THE FIRST THING YOU KNOW, Ol' Jed's a millionaire; the kinfolks said 'Jed, move away from there....'". Hope you all enjoyed it!
Originally posted by alamocdc
<br />Boo, hiss! I'm embarrassed that it was that simple.[:I]
Originally posted by MLKWoodWorking
<br />He becomes President?
Originally posted by Blind_Squirrel
<br />....Then, the monkey tries to climb the rope. What happens?
The monkey and the weight both rise at half the rate of the monkey's climb.Originally posted by Sylvanite
<br />[quoteA monkey hangs on a rope... What happens?
Originally posted by Fred_erick
<br />IF the rope is long enough and the monkey climbs high enough, the extra weight of the rope on the monkey's side will add to the weight of the monkey and the weight will reach the pulley on it's side and then the monkey can continue his climb and escape and get the <b>banana</b> that awaits his efforts.
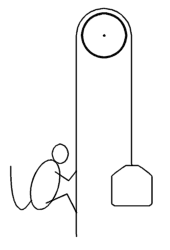
Originally posted by Blind_Squirrel
<br />A rope hangs over a pulley. On one end is a weight. Balanced on the other end is a monkey of equal weight. The rope weighs 4oz. per foot. The age of the monkey and the age of its mother together equal 4 years. The weight of the monkey is as many pounds as its mother is years old. The mother is twice as old as the monkey was when the mother was half as old as the monkey will be when the monkey is three times as old as the mother was when the mother was three times as old as the monkey. The weight of the weight plus the weight of the rope is half as much again as the difference between twice the weight of the weight and the weight of the monkey. How long is the rope?
Well, that was the steady-state solution. The dynamic analysis is somewhat more complicated and things change. The answer below assumes that this thought experiment occurs on Earth, so the non-Euclidean geometries and relativistic effects of a space-traveling monkey don't come into play. I'm also ignoring other minor variables, such as elasticity of the rope, angular momentum of the pulley, friction, coriolis force, atmospheric effects, and that the monkey is losing weight with exercise.Originally posted by LostintheWoods
<br />Eric has it.
Originally posted by Sylvanite
<br />Well, that was the steady-state solution. The dynamic analysis is somewhat more complicated and things change. The answer below assumes that this thought experiment occurs on Earth, so the non-Euclidean geometries and relativistic effects of a space-traveling monkey don't come into play. I'm also ignoring other minor variables, such as elasticity of the rope, angular momentum of the pulley, friction, coriolis force, atmospheric effects, and that the monkey is losing weight with exercise.Originally posted by LostintheWoods
<br />Eric has it.
Initially, as the monkey climbs, both he and the weight rise together. The higher he gets, however, the more rope is transfered from the weight side of the pulley to the monkey side. Eventually, that side is imbalanced to the point that the monkey starts moving downwards. It falls faster and faster until the weight reaches the pulley.
At that point, the weight and rope stop abruptly, ripping the rope out of the monkey's grasp and breaking most of his fingers in the process. The monkey falls to the ground beneath the pulley, landing on his head and giving it a severe concussion. Lying there in a daze, the monkey has mere seconds to look up and realize that the weight (now released) is hurtling back down. Frozen by shock and panic, the monkey cannot move and the weight crashes into his groin.
Some time later, when the monkey regains consciousness, he realizes that his constant migranes, double-vision, and broken hands will prevent him from ever using a lathe again. Emasculated and unable to turn pens, he grabs his turning tools and Tormek sharpener - and heads out on a 3-state killing spree.
The monkey hunts down everybody he has ever given or sold a pen to, skews, gouges, or scrapes them to death and steals back his work. Just when the Police, FBI, BATF, and INS have him cornered, the monkey mysteriously disappears, leaving behind nothing but a bloody termite hollowing tool. Rumours of random skewings still abound today.
The legend of the climbing monkey serves as the basis for a character in an upcoming Quentin Tarantino directed Batman movie -- an arch-villain known only as "The Chiseler".

