Who said Mathematics is a perfect science.

Signed-In Members Don't See This Ad
Bob Wemm

Bob Wemm

Member
Joined
Mar 9, 2012
Messages
1,994
Location
Kalbarri, Western Australia
Hi Guys and Gals,

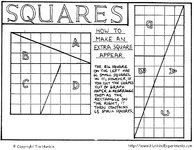
I don't know if anyone is interested but I can cut up a piece of paper 8inches square (64 sq inches) and refit the same pieces together exactly in a different shape and they measure 65 sq. inches.

When I went to school that was impossible, and I would love to hear from anyone who is interested or has an explanation of how this is possible.

Because I cannot explain it. ??????????????????

Bob.:confused:
 
Signed-In Members Don't See This Ad
This is a fun one! I've attached a graphic I found online to show the detail. And yes, there is an explanation .....
 

Attachments

  • image-1384320856.jpg
    image-1384320856.jpg
    223.4 KB · Views: 473
The drawing is misleading.

Take a look at the larger 65 sq inch picture where section C and B touch each other - from the bottom left corner to the upper right.

Part B slopes down at a rate of 3 blocks over 8 blocks or 3/8 which is .375.
Part C slopes at a rate of 2 blocks over 5 blocks or 2/5 which is .4.

So, if the larger picture was drawn more accurately there would be a small sliver of "new" space between sections C and B as well as A and D. This new space, while small, would in all likelihood add up to 1 square.

That's my guess - assuming John U's picture is what Mr. Bob was writing about.

Dave (minored in math a very long time ago)
 
Last edited:
lyonsacc said:
The drawing is misleading.

Take a look at the larger 65 sq inch picture where section C and B touch each other - from the bottom left corner to the upper right.

Part B slopes down at a rate of 3 blocks over 8 blocks or 3/8 which is .375.
Part C slopes at a rate of 2 blocks over 5 blocks or 2/5 which is .4.

So, if the larger picture was drawn more accurately there would be a small sliver of "new" space between sections C and B as well as A and D. This new space, while small, would in all likelihood add up to 1 square.

That's my guess - assuming John U's picture is what Mr. Bob was writing about.
Dave (minored in math a very long time ago)
Click to expand...


Dave, the picture is not really misleading, for the extra 1 sq. inch to be there between the two triangles there would have to be at least 1/16in gap all the way along. When I did my cut and fitup there was virtually no gap.

John, there has to be an explanation but lets see what develops here before you let the cat out of the bag.

Bob.
 
This reminds me of the old fun maths problem we did at school.
How many can remember this one? :)

Three people eat in a restaurant when finished, the waiter brings the bill for $30.
Each person puts in $10.
The waiter takes the money to the cashier who finds that the bill should have only been $25, so gives the waiter $5 change.

Now the waiter isn't good at maths and can't figure out how to split $5 between three so puts $2 in his pocket and gives each of them $1 each.

So, each person paid $10 and got back $1, so $9 each right?
3 x 9 = 27 plus the $2 in waiter's pocket
27 + 2 = 29

Where is the last missing dollar?????

:)
 
This is an accounting error, not a math one.
The meal cost 25 so 25 divided by 3 is 8 1/3 dollars each.
The dollar returned by the waiter makes the meal 9 1/3 dollars each.
So 9 1/3 times 3 plus 2 is the whole 30 dollars.

There still seems to be a dollar missing somewhere. I'm not an accountant.
Do a good turn daily!
Don





skiprat said:
This reminds me of the old fun maths problem we did at school.
How many can remember this one? :)

Three people eat in a restaurant when finished, the waiter brings the bill for $30.
Each person puts in $10.
The waiter takes the money to the cashier who finds that the bill should have only been $25, so gives the waiter $5 change.

Now the waiter isn't good at maths and can't figure out how to split $5 between three so puts $2 in his pocket and gives each of them $1 each.

So, each person paid $10 and got back $1, so $9 each right?
3 x 9 = 27 plus the $2 in waiter's pocket
27 + 2 = 29

Where is the last missing dollar?????

:)
Click to expand...
 
"3 x 9 = 27 plus the $2 in waiter's pocket"

the $2 is part of the $27, so it would not be added again

$27 + the $3 = $30


I like our Washington math (or my Wife LOL).

I was going to spend $800 Million dollars buying gadgets but only spent $600 million. I saved you $200 million
 
skiprat said:
This reminds me of the old fun maths problem we did at school.
How many can remember this one? :)

Three people eat in a restaurant when finished, the waiter brings the bill for $30.
Each person puts in $10.
The waiter takes the money to the cashier who finds that the bill should have only been $25, so gives the waiter $5 change.

Now the waiter isn't good at maths and can't figure out how to split $5 between three so puts $2 in his pocket and gives each of them $1 each.

So, each person paid $10 and got back $1, so $9 each right?
3 x 9 = 27 plus the $2 in waiter's pocket
27 + 2 = 29

Where is the last missing dollar?????

:)
Click to expand...

To confuse matters..............when my ex-sister-in-law was confronted with this question she was stuck on trying to figure out how the waiter was able to take two dollars from a five dollar bill:confused::rolleyes::tongue:

If mathematics were perfect we'd have no Pi. Make mine apple please :biggrin:
 
Akula said:
"3 x 9 = 27 plus the $2 in waiter's pocket"

the $2 is part of the $27, so it would not be added again

$27 + the $3 = $30


I like our Washington math (or my Wife LOL).

I was going to spend $800 Million dollars buying gadgets but only spent $600 million. I saved you $200 million
Click to expand...

It all depends on where you start from Hey.

The meal was $25 plus the $2 in the waiters pocket makes $27, and the three eaters had $1 each in their pocket so that makes $30.

But Where did the extra 1 Square inch come from???????

Bob.:confused::confused::confused::confused::confused::confused::confused::confused:
 
This is an accounting error, not a math one.
The meal cost 25 so 25 divided by 3 is 8 1/3 dollars each.
The dollar returned to each by the waiter makes the meal 9 1/3 dollars each.
So 9 1/3 times 3 plus 2 is the total 30 dollars.

There still seems to be a dollar missing somewhere. I'm not an accountant.
Do a good turn daily!
Don





skiprat said:
This reminds me of the old fun maths problem we did at school.
How many can remember this one? :)

Three people eat in a restaurant when finished, the waiter brings the bill for $30.
Each person puts in $10.
The waiter takes the money to the cashier who finds that the bill should have only been $25, so gives the waiter $5 change.

Now the waiter isn't good at maths and can't figure out how to split $5 between three so puts $2 in his pocket and gives each of them $1 each.

So, each person paid $10 and got back $1, so $9 each right?
3 x 9 = 27 plus the $2 in waiter's pocket
27 + 2 = 29

Where is the last missing dollar?????

:)
Click to expand...
 
Last edited:
Bob Wemm said:
lyonsacc said:
The drawing is misleading.

Take a look at the larger 65 sq inch picture where section C and B touch each other - from the bottom left corner to the upper right.

Part B slopes down at a rate of 3 blocks over 8 blocks or 3/8 which is .375.
Part C slopes at a rate of 2 blocks over 5 blocks or 2/5 which is .4.

So, if the larger picture was drawn more accurately there would be a small sliver of "new" space between sections C and B as well as A and D. This new space, while small, would in all likelihood add up to 1 square.

That's my guess - assuming John U's picture is what Mr. Bob was writing about.
Dave (minored in math a very long time ago)
Click to expand...


Dave, the picture is not really misleading, for the extra 1 sq. inch to be there between the two triangles there would have to be at least 1/16in gap all the way along. When I did my cut and fitup there was virtually no gap.

John, there has to be an explanation but lets see what develops here before you let the cat out of the bag.

Bob.
Click to expand...

John's explanation is correct. With the two slopes of the cut pieces being different, it is impossible for the hypotenuse of the two rearranged larger "triangles" to be straight lines. The rearranged drawing is an illusion. It is not accurate. Tape together each small triangle with its corresponding trapezoid. Then carefully fit the opposite corners of each larger "triangle" to make the larger figure. You'll see there is a gap going the length of the so called diagonal. Each of the two larger "triangles" are in fact two identical,but irregular four sided figures. The gap between the two taped pieces equals one square unit, as John suggested.
 
I will asked the Grandkids at dinner today the will figure it out. All 5 are great at math a talent they didn't get from me. I passed high school geometry by one point, that was enough to allow me to graduate. I have gotten better at math as I have become older but they beat me every time.
 
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
 
its_virgil said:
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
Click to expand...
The 1st son got 9/17 horses, the 2nd son got 6/17, and the youngest son got 2/17 horses. Not exactly as the old rancher that died had laid it out in his will, but close enough I guess!
 
Last edited:
its_virgil said:
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
Click to expand...

1/2 = 3/6
1/3 = 2/6
1/6 = 1/6
+___
6/6
 
Sorry, I made a mistake. The 1/6 should have been 1/9. Then 1/2 + 1/3 + 1/9 = 9/18 + 6/18 + 2/18 = 17/18 . The fractional parts must equal one (1). I guess if the sons were happy then all is good. My typo ruined the question.
Don

Mr Vic said:
its_virgil said:
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
Click to expand...

1/2 = 3/6
1/3 = 2/6
1/6 = 1/6
+___
6/6
Click to expand...
 
pwhay said:
Hi Bob,

You cant get kittens from a cat named George. I can explain that.

All that glitters is not Gold.

Kind regards Peter.
Click to expand...

Peter:
I respectfully disagree! You can, in fact, get kittens from a cat named George. I propose that possibly one half of all cats named George by three year old children, can, in fact, produce kittens:) DAMHIKT:)
 
OK, it seems that you cannot turn 64 into 65.
Dave, please accept my apologies, the diagram is indeed very misleading.
I have attached two images, firstly 8 inches square with the division into 4 pieces.
The second image is a graph of 2 in. squares and the appropriate enlarged pieces drawn in.
There is indeed a "Spare" piece between the two triangles. When I tried this years ago I obviously didn't cut my paper straight enough.

My excuse is I only went to year 10 at school, and I'm sticking to that.

I hate it when I'm wrong. That's the second time.

At least we have learned about never ending Chocolate blocks, Horse divisions and a few other things. Thanks for participating. Oh, I nearly forgot George the Cat.

Bob.:biggrin::biggrin:
 
lyonsacc is right, very small amount of space is introduced due to the difference in slopes.
You can see it in this accurate picture.
squares.jpg

In the change/waiter problem the $9 they each paid was for the meal (25/3) and the money the waiter kept (2/3).
Each person paid $25/3 + $2/3 = $27/3 = $9


The horses problem, the cowboy in adding his horse made the number of horses 18 which is evenly divisible by 2, 3, and 6. It also caused all the results to round up and then round back down when they took away his horse from the results. Though the final result was a bit unfair for the youngest son, he should of gotten 2.83 (17/6) horses but only got 2. Perhaps the split should of been 8, 6, 3 :smile:

Love to have a chocolate block like that. Unfortunately it's a trick, the bottom of the diagonally cut sections grow as they move to make full rectangles of chocolate.

Just love solving puzzles :biggrin:

TonyO
 
Sometimes things just do not go right.
Sorry about forgetting to post the photos.
I would probably forget my head if it wasn't joined on.
Bob.
:redface::redface::redface:



Bob Wemm said:
OK, it seems that you cannot turn 64 into 65.
Dave, please accept my apologies, the diagram is indeed very misleading.
I have attached two images, firstly 8 inches square with the division into 4 pieces.
The second image is a graph of 2 in. squares and the appropriate enlarged pieces drawn in.
There is indeed a "Spare" piece between the two triangles. When I tried this years ago I obviously didn't cut my paper straight enough.

My excuse is I only went to year 10 at school, and I'm sticking to that.

I hate it when I'm wrong. That's the second time.

At least we have learned about never ending Chocolate blocks, Horse divisions and a few other things. Thanks for participating. Oh, I nearly forgot George the Cat.

Bob.:biggrin::biggrin:
Click to expand...
 

Attachments

  • 008.JPG
    008.JPG
    67.2 KB · Views: 134
  • 009.JPG
    009.JPG
    59.4 KB · Views: 124
No worries Bob.

My 11 and 9 year old are with me at work today. I am going to pose the problem to them to see if they can figure it out.

Dave
 
its_virgil said:
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
Click to expand...
Easily. The total number of horses left was 17 but the division in the will was 17/18 so you could add one horse and give each of the sons more than they had actually been left and still have one horse left at the end.
 
its_virgil said:
Sorry, I made a mistake. The 1/6 should have been 1/9. Then 1/2 + 1/3 + 1/9 = 9/18 + 6/18 + 2/18 = 17/18 . The fractional parts must equal one (1). I guess if the sons were happy then all is good. My typo ruined the question.
Don

Mr Vic said:
its_virgil said:
An old rancher died and left 17 horses to his three sons. The oldest was to inherit 1/2 of the horses. The middle son was to inherit 1/3 of the horses and the youngest to inherit 1/6 of them. As they were sitting on the corral fence debating how to divide the horses (without fractional horses) an old cowboy rode up and asked what they were doing. After telling the old cowboy of their problem the old cowboy put his horse in the corral. Now there were 18 horses in the corral. He told the oldest to take 9 horses but to leave his. He told the middle son to take 6 horses but leave his. And the youngest son took 2 horses and left the old cowboy's horse. The old cowboy got on his horse and rode off. What is the problem with this thinking or how did it work?

I often gave this question as a bonus question on tests after teaching about fractions, proportions and percents.

Do a good turn daily!
Don
Click to expand...

1/2 = 3/6
1/3 = 2/6
1/6 = 1/6
+___
6/6
Click to expand...
Click to expand...
Why wouldn't they be happy they all got more than they should have 1.e. son #1 was entitled to 1/2 of 17 horses or 8 1/2 horses and got 9 - son #2 was entitled to 1/3 of 17 horses or 5 2/3 horses and got 6 - son #3 was entitled to 1/9 of 17 horses or 1 8/9 horses and got 9. What's to be unhappy about.
 
Some people are never happy, no matter what they get.

We were talking to our daughter the other day about winning the lotto. Betty said she would give Nikki $1,000,000 if we won. Nikki said, "Is that all"???

Bob.
 
Bob Wemm said:
Some people are never happy, no matter what they get.

We were talking to our daughter the other day about winning the lotto. Betty said she would give Nikki $1,000,000 if we won. Nikki said, "Is that all"???

Bob.
Click to expand...

Gee Bob,

If you won the lotto I'd be willing to be your second cousin for a mere $50,000.
 
Signed-In Members Don't See This Ad
Why wouldn't they be happy they all got more than they should have 1.e. son #1 was entitled to 1/2 of 17 horses or 8 1/2 horses and got 9 - son #2 was entitled to 1/3 of 17 horses or 5 2/3 horses and got 6 - son #3 was entitled to 1/9 of 17 horses or 1 8/9 horses and got 9. What's to be unhappy about.
Click to expand...

The issue is the last son didn't get what he was deserving.

1/6 of the horses x 17 horses = 2.83 horses. He was shorted by almost an entire horse.

The other two took a portion more than they were entitled.
 
Last edited:
You must log in or register to reply here.
Back
Top Bottom